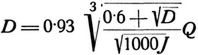- Lichtweite
Lichtweite der Brücken und Durchlässe (spart, clear width; ouverture libre; luce), gemessen zwischen den Widerlagsmauern oder Pfeilern, u.zw. in dazu senkrechter Richtung von Pfeilerflucht zu Pfeilerflucht. Von der L. zu unterscheiden ist die Stützweite, die von Mitte zu Mitte der Auflager des Brückentragwerks gemessen wird und stets größer als die L. ist.
Die L. einer Brücke ist in vielen Fällen schon durch die Breite des zu übersetzenden Objektes, des durchzuführenden Weges oder Wasserlaufes gegeben oder es ist für den Verkehr unter der Brücke eine gewisse kleinste L. notwendig.
Bei der Überbrückung von Eisenbahnen ist das Lichtraumprofil (s.d.) maßgebend, das für die dem VDEV. angehörenden Bahnlinien durch die TV. (§ 30) festgesetzt ist. Danach ist bei Überbrückung einer mehrgleisigen Vollbahn von der Achse jedes äußeren Gleises, mit Hinzurechnung eines Spielraumes von 20 cm, eine Weite von mindestens 2∙20 m freizuhalten. Liegt das Gleis an der Überbrückungsstelle in einem Bogen, so ist auf die durch die Schiefstellung des Lichtraumprofils bedingte Vergrößerung des obigen Maßes Rücksicht zu nehmen. Danach erfordern Überbrückungen eingleisiger Bahnen ohne Durchführung der Bahneinschnittsgräben mindestens 4∙4 m L. Sollen die Bahneinschnittsgräben innerhalb der Brückenöffnung durchgeführt werden, so ist die L. auf 6 m, bzw. 7∙2 m zu vergrößern, je nachdem die Gräben ein gemauertes Profil oder bahnseitig Erdböschungen erhalten. Für die Überbrückung zweigleisiger Bahnen ergeben sich als Mindestmaße der L. ohne Gräben 8 m, mit Durchführung der Gräben 10 m, bzw. 11∙2 m.
Bei Straßenüberbrückungen ist die L. durch die Straßenbreite bestimmt; dabei ist bei Landstraßen eine Einschränkung um die Bankettbreite, d.i. um etwa 1 m meist zulässig. Auch kann die Führung der Straßengräben, wenn solche vorhanden sind, längs der Widerlager in gemauerten Gerinnen oder durch die Widerlager selbst erfolgen, um die Brückenweite einzuschränken. Durchschnittlich beträgt die Straßenbreite in Deutschland und Österreich
für Reichs- und Landesstraßen 10 – 15 m für Bezirksstraßen 6 – 8 m für Gemeindestraßen 4 – 5 m für Feldwege 3 m für Fußwege 1∙5 – 1∙8 m
Bei Überbrückung eines in ein regelmäßiges Gerinne gefaßten Wasserlaufes, z.B. eines Mühlgrabens, bestimmt dessen Breite von selbst die L. der Brücke. Man kann nur zuweilen eine Verminderung der Weite dadurch erreichen, daß man das Gerinne unter der Brücke anstatt mit Erdböschungen mit gemauerten Einfassungen versieht. Bei Brücken über Schiffahrtskanälen empfiehlt es sich nicht, die Wasserspiegelbreite einzuschränken. So erhielten am Rhein-Herne-Kanal, der eine Wasserspiegelbreite von 34∙5 m besitzt, die Brücken durchweg eine Lichtweite von 54 m. Seeschiffahrtskanäle erfordern entsprechend große Brückenlichtweiten. Die Brücken über den Nordostseekanal z.B. haben mindestens 60 m, meist aber größere L. erhalten.
Brücken über fließende Gewässer sowie auch Durchlässe und kleinere Brücken, die nur zur Entwässerung eines kleinen Niederschlagsgebietes dienen, erfordern zur Festsetzung ihrer L. die Rücksichtnahme auf eine unbehinderte Hochwasserabfuhr und zu diesem Zwecke Erhebungen über die durch den Brückenquerschnitt abzuführenden Hochwassermengen. In manchen Fällen kann hier die L. nach in der Nähe befindlichen, denselben Wasserlauf überspannenden Brücken bestimmt werden, wenn sich diese als richtig bemessen erwiesen haben.
Für kleine Brücken und Durchlässe genügt es, die abzuführende Hochwassermenge schätzungsweise aus der Größe des Niederschlagsgebietes zu ermitteln. Hierzu kann die von Kresnik aufgestellte Formel benutzt werden:
1)
Hierin bezeichnet A das Niederschlagsgebiet in km2 (für kleine Gebiete mindestens = 1), W die sekundliche Hochwassermenge in m3; der Koeffizient α ist für Katastrophenhochwasser = 1 und sinkt nur bei besonders abflußverzögernden Verhältnissen bis auf etwa 0∙6; für gewöhnliches Hochwasser ist α = 0∙2 bis 0∙3. Diese Formel stimmt auch gut mit der Hochwassertabelle von Pascher (Ztschr. d. Österr. Ing.-V. 1892) überein. Die gesamte Hochwassermenge ist danach
Q = A ∙ W in m3 i. d. Sek. 2)
Man rechnet sonst auch als gewöhnliches Hochwasser i. d. Sek.
i. 1 km2 für Wildbäche 6–8 m3 für Bäche mit einer Tallänge von 4– 8 km 4 m3 für Bäche mit einer Tallänge von 8–12 km 3 m3 für Bäche mit einer Tallänge von 12–16 km 2 m3
doch können bei außergewöhnlichen Hochwässern diese Abflußmengen auch erheblich, bis aufs doppelte, größer werden.
Aus der Abflußmenge Q bestimmt sich bei der mittleren Geschwindigheit v des Hochwassers und mit dem Kontraktionskoeffizienten μ die Fläche des Durchflußquerschnittes F aus
F = Q/μv
und bei der Wassertiefe t die lichte Durchflußweite L der Brücke oder des Durchlasses
L = F/t = Q/μvt 3)
Die Geschwindigkeit v läßt sich aus v = 50 √RJ berechnen, worin J das Gefälle, R den hydraulischen Radius (Fläche F: benetzten Umfang U) bezeichnet. Man erhält damit, wenn bei rechteckigem Durchflußprofil t = 1/2L bis 1/4L
4)
Der Koeffizient μ ist für Durchlässe im Flachlande mit geringer Sohlenneigung mit 0∙8, für stark geschiebeführende Wasserläufe im Gebirge mit 0∙5 anzunehmen.
Für Durchlässe für kleinere Wasserläufe kann man auch Formel 3) verwenden und darin folgende Mittelwerte von v einsetzen:
bei einem Gefälle des Talgerinnes > 0∙01 v = 3∙5 m bei einem Gefälle des Talgerinnes 0∙01–0∙005 v = 3∙1 m bei einem Gefälle des Talgerinnes < 0∙005 v = 2∙1 m
Der lichte Durchmesser D kreisförmiger Rohrdurchlässe ist bestimmt durch
5)
Ist das natürliche Gefälle eines Wasserlaufes gering und eine künstliche Vergrößerung nicht ausführbar oder ist das Gerinne so wenig tief eingeschnitten, daß das Hochwasser eine breite Fläche überflutet, so ist man entweder nur mit unverhältnismäßig großem Kostenaufwande oder überhaupt nicht in der Lage, das Wasser ohne Stauung abzuleiten. Die Stauhöhe vergrößert sich in dem Maße, als die lichte Durchflußweite verringert wird; gleichzeitig vergrößert sich damit auch die Durchflußgeschwindigkeit im Brückenquerschnitt. Es kann nun entweder das zulässige Maß der Stauhöhe durch die erlaubte Inundation des Geländes begrenzt sein oder es darf eine gewisse größte Geschwindigkeit im Flußgerinne nicht überschritten werden, damit dessen Sohle gegen die Angriffe des Wassers geschützt bleibt. Hierauf ist bei allen Brücken Bedacht zu nehmen, bei denen die Wasserspiegelbreite durch in den Fluß gestellte Pfeiler eingeengt wird.
Ist s die Stauhöhe vor der Brücke, h = v2/2g die Geschwindigkeitshöhe des mit der Geschwindigkeit v ankommenden Wassers im gestauten Querschnitt, t die Tiefe des ungestauten Wassers, L die gesamte Durchflußweite im Brückenquerschnitt, so erhält man mit dem Kontraktskoeffizienten μ die Wassermenge aus:
6)
oder mit meist hinreichender Annäherung
7)
Die mittlere Geschwindigkeit im Brückenquerschnitt bestimmt sich aus
v1 = Q/μLt 8)
die Geschwindigkeit im gestauten Profil oberhalb der Brücke bei der Fläche F aus
v = Q/F
Näherungsweise ergibt sich damit die Stauhöhe s
9)
Der Kontraktionskoeffizient μ kann bei rechteckigem Pfeilergrundriß mit 0∙8, bei rundem oder spitzbogigem Pfeilervorkopf mit 0∙95 angenommen werden. Für die Geschwindigkeit v1 können erfahrungsgemäß folgende Höchstwerte zugelassen werden:
Holzgerinne 10 m Felsboden oder gemauertes Gerölle 5–8 m Grobes festgelagertes Gerölle 4 m Mittleres festgelagertes Geschiebe 3 m Kies 2 m Sand 1 m Fester Lehmboden mit Rasen 3 m
Die vorausgesetzte Beschaffenheit des Gerinnes muß aber nicht bloß unter der Brücke, sondern auch in einer entsprechend langen Strecke oberhalb und unterhalb vorhanden sein. Wo es sich um sehr geringe Wassermengen handelt, können ohne Bedenken auch noch größere Geschwindigkeiten, als oben angegeben, zugelassen werden.
Mit Hilfe der Formeln 6–9 kann die erforderliche Durchflußweite einer Brücke bestimmt werden, so daß entweder eine gegebene Stauhöhe oder eine gewisse Durchflußgeschwindigkeit nicht überschritten wird.
Bei einer größeren Strombrücke bleibt dann noch die Aufgabe zu lösen, wie diese Gesamtweite in die Einzelöffnungen aufzuteilen oder wie groß deren Zahl zu wählen ist. Auch bei Talbrücken und Viadukten wird die Frage nach der zweckmäßigen Größe der Einzelöffnungen zu beantworten sein. Bei schiffbaren Flüssen werden Rücksichten auf den Wasserverkehr bestimmte Lichtmaße erfordern. Im übrigen sind aber die Öffnungsweiten einer Brücke unter dem Gesichtspunkte der Erzielung des kleinsten Kostenaufwandes auszuteilen. Es ist klar, daß man umso größere Einzel-Lichtweiten wählen wird, je schwieriger und teurer die Pfeilerbauten sind und je weniger rasch die Kosten des Brückenüberbaues f. d. m Länge mit der Spannweite an wachsen. Bestimmte allgemeine Angaben lassen sich hiefür nicht machen; man wird in einem gegebenen Falle nur durch den Vergleich einiger Lösungen zu der wirtschaftlich günstigsten Anordnung gelangen.
Melan.
http://www.zeno.org/Roell-1912. 1912–1923.