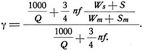Virtuelle Länge

Virtuelle Länge (virtual length; longueur virtuelle; lunghezza virtuale). Die V., auch Betriebs- oder Vergleichslänge genannt, ist die Länge einer gedachten, meist einer wagrechten, geraden, ausnahmsweise einer schwach geneigten Bahn, welche die gleichen Betriebserschwernisse verursacht wie eine bestehende oder geplante Bahn. Die V. kann ermittelt werden für gleiche Widerstandsarbeit, gleiche Zugkraftskosten, gleiche, teilweise oder gesamte Betriebskosten, auch gleiche Fahrzeiten. Diejenige Länge einer gedachten Bahn, welche die gleichen Einnahmen liefern würde wie die geplante Bahn, bezeichnet man als Tariflänge. Zum Vergleich mehrerer Bahnen, die gleichen Zweck verfolgen und etwa die gleichen Endpunkte verbinden aber verschiedene Neigungs- und Krümmungsverhältnisse in bezug auf Größe und Länge erhalten sollen, also zum Vergleich sog. Varianten, wird, namentlich für schwierige Bahnen im Gebirge, die V. für gleiche Widerstandsarbeit oder für gleichen Kraftverbrauch herangezogen. Als Vergleichsgrundlage soll eine wagrechte und gerade Bahn angenommen werden. Bezeichnet l die wirkliche Länge der geplanten und l_v die V., also die Länge der gedachten Bahn, so ist

l_v = C ∙ l; C = l_v/l

der virtuelle Beiwert. Bei Trennung der Einflüsse von Steigungen und Krümmungen erhält man

für die Steigungen l'_v = al,

für die Krümmungen l"_v = b ∙ l,

die Verlängerung der geplanten Bahn ist daher

l'_v – l = al – l,

l"_v – l = bl – l,

l_v = l + (al – l) + (bl – l) = (l a + b – 1).

Für gleiche Widerstandsarbeit kann man für ganz annähernde schätzungsweise Ermittlung der V. ausgehen von den Gleichungen:

Für Steigungen:

Für Krümmungen:

Es bezeichnen W_o, W_S, W_c die Laufwiderstände in der wagrechten, geneigten und gekrümmten Strecke und S das Neigungsverhältnis der Bahn. Annähernd kann man im vorliegenden Fall für Güterzüge mit geringer Geschwindigkeit W_o = W_s setzen. Für gleiche Neigung S kann man die V. für Steigungen und Krümmungen annähernd annehmen mit:

Setzt man W = 3, was für Güterzüge im Durchschnitt zutrifft, und annähernd W_c = 600/R, worin R den Krümmungshalbmesser der Gleisachse bezeichnet, so erhält man die für Schätzungen gebrauchte Formel:

worin + für Steigungen, – für Gefälle zu setzen ist.

Für gleiche Widerstandsarbeit erhält man ein etwas zutreffenderes Maß für die V. auf Grund nachstehender Rechnung:

1. Z_o = (Q + G_o)^t W_o^kg/t für gerade wagrechte Bahn;

2. Z = (Q + G)^t ∙ (W_s ± S)^kg/t für gerade geneigte Bahn. Es bezeichnen Z_o und Z die Zugkräfte auf wagrechter und geneigter Bahn, Q das Lokomotivgewicht, G_o das Zuggewicht auf wagrechter Bahn, G das Zuggewicht auf geneigter Bahn, W_o und W_s die Laufwiderstände auf wagrechter und geneigter Bahn, die sich mit der Fahrgeschwindigkeit ändern, S den Steigungswiderstand. Für die Gleichheit der Zugkräfte erhält man:

3. (Q + G_o) W_o = (Q + G)(W_s ± S), hieraus

4. G/G_o (W_s ± S) = Q/G_o (W_o – W_s ∓ S) + W_o, daher die V.

5.

da Z_o = Z = Qnf = (Q + G_o)W_o, worin bezeichnen n den Faktor, der angibt, wieviel des Gesamtgewichts der Lokomotive auf das Reibungsgewicht entfällt, wobei für Dampflokomotiven meist n = 0∙5–1∙0, für elektrische Lokomotiven n = 0∙7–1∙0 angenommen werden kann, f den Reibungswert, den man für Dampfbetrieb mit 145–150‰, für elektrischen Betrieb mit 165–170‰ annimmt. Die Annahme größerer Reibungswerte ist nur in besonders günstigen Fällen zulässig. Setzt man den Wert Qnf in Gleichung 5, so erhält man

6.

die V. für Neigungen bei l Länge der geplanten Bahn. Für langsam fahrende Güterzüge kann man W_o = W_s = W setzen, daher:

7.

Für die Fahrt im Gefälle oder die Talfahrt wird S negativ. Solange S kleiner ist als die Grenze der unschädlichen und schädlichen Neigung, d.i. die Bremsneigung, ist Zugkraftarbeit erforderlich; der virtuelle Beiwert ist daher größer als Null. Wird S größer als die Bremsneigung, dann ist keine Zugkraftarbeit, sondern nur Bremsarbeit nötig. Im letzteren Fall kann man die Kosten der Bremsarbeit sowie den stärkeren Schienen- und Radverschleiß in Rechnung stellen.

Die Bahnstrecke wird in Teile geteilt, in welchen gleiche Neigungen vorhanden sind; für die entsprechenden Streckenteile werden die V. sowohl für die Hin- wie für die Rückfahrt bestimmt und hieraus der Durchschnitt ermittelt. Für gekrümmte Strecken kann man den Widerstand W_s + S um den Krümmungswiderstand W_c vergrößern, so daß eine besondere Rechnung erspart werden kann. Für Bahnen von gleichem Widerstand, bei welchen in den gekrümmten Strecken die Größtneigung S um das Maß W_c des Krümmungswiderstands vermindert wird, ist eine besondere Berücksichtigung der Krümmungen nicht erforderlich, sobald die V. auch in den gekrümmten Strecken für die Größtneigung S ermittelt wird.

Unabhängig hiervon kann die V. für die Krümmungen ermittelt werden aus Gleichung

8.

worin

den Krümmungswiderstand bezeichnet. Aus Gleichung 6 folgt, daß unter sonst gleichen Verhältnissen die V. l'_v für elektrischen Betrieb kleiner, also günstiger ist wie für Dampfbetrieb, da im ersten Fall der Reibungswert f infolge gleichförmigen Antriebsdrehmoments und auch n wegen Fortfalls des Tenders sowie die Fahrgeschwindigkeit in der geneigten Strecke größer sind wie beim Dampfbetrieb.

Wenn auch die V. von Vergleichlinien oder Varianten, d.i. von Eisenbahnlinien, die den gleichen Zweck verfolgen, also auch zumeist die gleichen Endpunkte miteinander verbinden, nach den Gleichungen 7, 8, und 9 auf Grund gleicher Widerstandsarbeit oder gleichen Kraftverbrauchs ermittelt werden, was mit Rücksicht auf die sonstigen, nicht in Rechnung zu stellenden Ungenauigkeiten und den Umstand, daß die Neigungsverhältnisse wenig voneinander abweichen, meistens auch genügt, so sind für den Vergleich bei schärferer Beurteilung alle Kosten in die Rechnung einzubeziehen, die von den Steigungsverhältnissen abhängig sind. Mutzner (s. Lit.) hat ein Verfahren für die Ermittlung der V. mit Berücksichtigung der Transport- und Bahndienstkosten angegeben. Er teilt die betreffende Linie in Abschnitte, innerhalb welcher ungefähr gleiche Belastungen vorkommen. Die einzelnen Strecken mit verschiedenen Neigungen werden dann besonders behandelt, da auf Strecken mit kleinerer Steigung als der größten oder maßgebenden doch nur die Nutzlast, die auf dieser möglich ist, gefördert werden kann. Setzt man in Gleichung 6 S = S_m und W_s = W_m (Laufwiderstand auf maßgebender Steigung) und berücksichtigt den Krümmungswiderstand durch Zuschlag zu den Steigungen, so erhält man:

9.

Für flachere Steigungen S als die maßgebende S_m wird der virtuelle Beiwert C abgemindert durch einen Faktor γ, der von Mutzner, dann aber von Weber (s. Lit.) in verkürzter und, infolge ohnehin nur ungenauer Unterlagen, in ausreichend genauer Form angegeben wird mit:

10.

In Gleichung 10 bezeichnen Q das Dienstgewicht der Lokomotive, n das Verhältnis Q₁/Q von Triebradbelastung zum Dienstgewicht, wie schon bei Gleichung 6 angegeben, f den Reibungswert, S die Bahnneigung, kleiner als die maßgebende S_m, W_s und W_m die Laufwiderstände in beiden Fällen, ³/₄ das Verhältnis der proportional der indizierten Zugkraft wachsende Teil der Transportkosten für 1 t Zugkraft und 1 km zu dem von der Arbeitsleistung der Lokomotive unabhängigen Teil der Transportkosten für 1 t Zugkraft und 1 km.

Für das Gefälle wird für die Bremsneigung (W_s – S) = 0, hiernach

11.

also ein von der maßgebenden Steigung unabhängiger Wert. Für Neigungen, die die Bremsneigung, also die Grenze zwischen schädlicher und unschädlicher Neigung, überschreiten, wird in Gleichung 10 der Ausdruck

negativ, daher nimmt γ mit zunehmender Neigung weiter ab. Solange die Steigung die Bremsneigung nicht überschreitet, sind Zugkräfte erforderlich, darüber hinaus nur Bremskräfte.

Literatur: Lindner, Die virtuelle Länge und ihre Anwendung auf Bau und Betrieb der Eisenbahnen. Zürich 1879. – Melan, Zur Frage der virtuellen Länge. Wschr. d. öst. Ing. u. Arch.-Ver. 1879. – Launhardt, Theorie des Trassierens. Hannover 1887. – Baum, Des longueurs virtuelles. – Kreuter, Linienführung der Eisenbahnen. Wiesbaden 1900. – Rühle v. Lilienstern, Die Betriebslänge. Organ 1908. – Mutzner, Die virtuellen Längen der Eisenbahnen. Zürich 1914. – Kummer, Energetische Koeffizienten der virtuellen Längen von Bahnen, insbesondere bei elektrischem Betrieb. Schwz. Bauztg. 1916. – Steiner, Die virtuellen Längen bei elektrisch betriebenen Bahnen. Zürich 1919. – Weber, Die virtuellen Längen für Eisenbahnen. Verkehrstechnik. Berlin 1920. – Örley, Die maßgebende Arbeitshöhe der Eisenbahnen. Organ 1922.

Dolezalek.